动态规划(1)

总字数 1.6k

预计阅读时间 6 分钟

楔子

最大子序和 ( leetcode题目 )
给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:
输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

题目只需要求最大的和是多少, 而不需要知道这个子数组的起止位置
首先需要明确的是, 如果这个子数组的边缘位置(第一个或最后一个)元素是一个负数
那么这个子数组的和肯定不是最大的, 因为舍掉这个元素, 之后的和肯定会更大, 负数是会让总和减小的
比如[-3,4,-1,2] 这个子数组肯定不是最大, 因为把-3舍掉会更大

更进一步, 如果这个子数组边缘位置连续多个数的和是负数, 那么这多个数也可以舍掉, 让总和更大
比如[1,-3,4,-1,2] 这个子数组肯定不是最大, 因为把1,-3舍掉, 可以让总和更大

以示例当中给出的数组进行推演
[-2,1,-3,4,-1,2,1,-5,4]
( 下面的每个序号代表推进到第几个元素 )

1. 总和初始值是0 , 先加第一个数此时总和是-2
2. 前面的总和-2, 加上它会使总和 变小, 所以不加, 总和 归零, 然后加1, 此时总和是1
3. 前面的总和1, 加上它会使总和 变大, 所以加上, 此时总和是-2
4. 前面的总和-2, 加上它会使总和 变小, 所以不加, 总和 归零, 然后加4, 此时总和是4
5. 前面的总和4, 加上它会使总和 变大, 所以加上, 此时总和是3

…..
每一步是否舍弃前面总和的判断条件就是前面的总和是正还是负, 正数则加, 负数则舍弃
依次进行下去, 从每一步得到的总和里面找出最大的就可以了
每一步的总和分别是-2 1 -2 4 3 5 6 1 5
显然最大的是6

代码实现

class Solution {
  public int maxSubArray(int[] nums) {
    if(nums.length == 0) { //特殊情况判断
      return 0;
    }
    int sum = nums[0], maxSum = nums[0];
    for(int i=1 ; i<nums.length ; i++) {
      sum = (sum < 0 ? nums[i] : sum + nums[i]);
      if(sum > maxSum) {
        maxSum = sum;
      }
    }
    return maxSum;
  }
}

空间复杂度是O(1), 因为使用了常数个变量, 没有开辟长度为n的新数组
时间复杂度是O(n), 因为要逐个遍历传入的数组当中的元素

不同路径问题

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）
问总共有多少条不同的路径？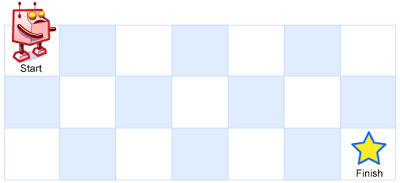

解决方式

1. 首先最左上角的格子的到达方式肯定只有1种, 因为必须要从这个格子开始走
2. 在每个格子当中只能向右或者向下移动, 所以每个对于每个格子来说, 到达这个格子的时候, 只能从左侧或者上方到达
3. 左边缘的格子无法从左侧到达, 上边缘的格子无法从上方到达

所以对于每个格子来说, 到达这个格子的路径的数量 = 到达左侧格子的数量 + 到达上方格子的数量
左边缘的格子前者为0, 上边缘的格子后者为0

根据这个原则, 就可以把到达每个格子的路径数量递推出来了

代码实现

public int uniquePaths(int m, int n) {
  if(m<=0 || n<=0) {
    return 0;
  }
  int[][] nums = new int[m+1][n+1];
  nums[1][1] = 1; // 起点方格的走法
  for(int i=1 ; i<=m ; i++) {
    for(int j=1 ; j<=n ; j++) {
      if(i==1 && j==1) {
        continue;
      }
      nums[i][j] = nums[i-1][j] + nums[i][j-1];
    }
  }
  return nums[m][n];
}

整体思路就是创建一个整数二维数组, m+1和n+1是为了留出第一行和第一列数值都是0
方便进行计算, 当然这个也不是必须的, 在循环当中判断也可以, 但是不影响时间和空间复杂度
时间复杂度O(mn)
空间复杂度O(mn)

进阶

如果某些方格存在障碍物, 机器人不能经过这些格子
有多少走法该如何计算
传入的参数是一个整数二维数组, 其中0代表该位置无障碍, 1代表该位置有障碍

这个问题同样可以沿用上一题的解法
需要补充的就是在障碍物的位置, 右侧和下方的格子
其对应的来自左侧和上面的走法应该是0, 因为无法从障碍物走过来

代码实现

public int uniquePathsWithObstacles(int[][] obstacleGrid) {
  int m = obstacleGrid.length;
  if(m == 0) {
    return 0;
  }
  int n = obstacleGrid[0].length;
  // 需要排除宽度是0以及高度是0的情况, 这种情况下走法是0
  // 还需要排除起点位置有障碍和终点位置有障碍的情况, 这种情况下走法也是0
  if(n == 0 || obstacleGrid[0][0] == 1 || obstacleGrid[m-1][n-1] == 1) {
    return 0;
  }
  int[][] nums = new int[m+1][n+1];
  nums[1][1] = 1;
  for(int i=1 ; i<=m ; i++) {
    for(int j=1 ; j<=n ; j++) {
      if(i == 1 && j == 1) {
        continue;
      }
      // 判断左侧是否有障碍
      int left = (i > 1 && obstacleGrid[i-2][j-1] == 0) ? nums[i-1][j] : 0;
      // 判断上方是否有障碍
      int top = (j > 1 && obstacleGrid[i-1][j-2] == 0) ? nums[i][j-1] : 0;
      nums[i][j] = left + top;
    }
  }
  return nums[m][n];
}

总结

动态规划的主要应用于使用穷举去解决时间复杂度过高的问题
将大问题化解为小问题, 并且记住前面小问题的求解结果, 避免在穷举过程中对前面小问题的重复求解
从而降低时间复杂度