阵列
二维阵列是最简单的数据结构, 我们可以把关系型数据库的一个表的内容看做一个阵列
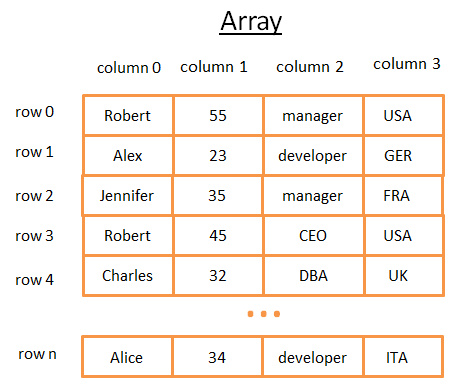
- 每行代表一个主体
- 列用来描述主体的特征
- 每个列保存的是某一种类型的数据 ( 整数/字符串/日期时间… )
如果采用这种方法保存数据 , 如果要一次性获得所有的数据十分方便 , 但是如果要查找特定的值
就要逐条记录进行遍历
在最不利的情况下 , 需要执行n次运算
时间复杂度1是O(n)
时间复杂度是一个函数,它定量描述了该算法的运行时间。这是一个关于代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,它考察当输入值大小趋近无穷时的情况。
如果想要检索的速度更快一些 , 就需要用到二叉树结构
树与数据库索引
二叉查找树是具有特殊属性的二叉树 , 其中的每个节点都代表了一条记录的数据 , 并且要满足如下要求
- 比保存在其左子树的任何键值都要大
- 比保存在其右子树的任何键值都要小
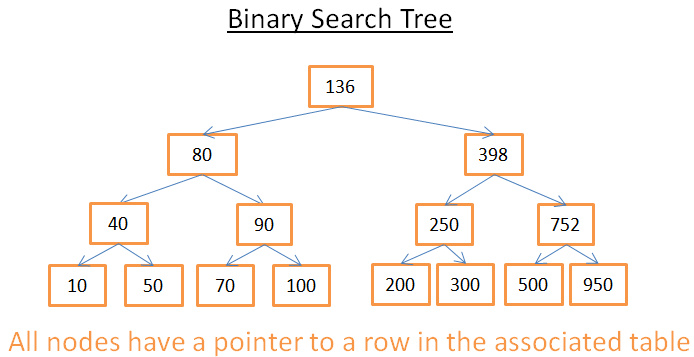
如果要在二叉查找树中搜索一个值, 首先与根节点比较, 如果值比根节点的值小, 那么就去找左子树, 反之去找右子树
再与子树的根节点比较, 依次进行下去
最终结果可能是在某个节点找到了这个值
或者需要进入下一个子树时, 已经没有子树
那么就代表这个值在树当中不存在
比如说我要找208 , 步骤如下:
- 从键值为 136 的根开始,因为 136<208,我去找节点136的右子树。
- 398>208,所以我去找节点398的左子树
- 250>208,所以我去找节点250的左子树
- 200<208,所以我去找节点200的右子树。但是 200 没有右子树,值不存在(因为如果存在,它会在 200 的右子树)
如果有n个数据 , 那么二叉树的深度就是log2(n)
所以这个查询的时间复杂度就是O(log2(n))
相当于一个等比数列求和, 首项是1, 公比是2, 总共有n项
根据等比数列的求和公式
代入可知 S = 2n-1
当n趋向于正无穷 , S = 2n , 所以 n = log2(S)
这里的S就表示集合当中的数据总数, n就表示进行一次查询的节点访问次数
这种二叉查找树就是一个数据库索引的模型
当然, 如果直接套用上述的方式, 只能解决快速的精确查询(针对某个特定值的), 如果要查找某个范围内的值, 仍然需要遍历整个树
B+树索引
为了解决查找某个范围内的值的问题, 需要找到高效的范围查询的方法, 现代数据库使用了一种修订版的二叉查找树, 称为B+树
这种树结构有如下特点
- 只有叶子节点才保存信息(根据其中的信息可以直接找到表中对应的行)
- 其他节点只是在搜索中用来指引到正确节点的
- 临近的叶子节点是相连的, 构成链表结构
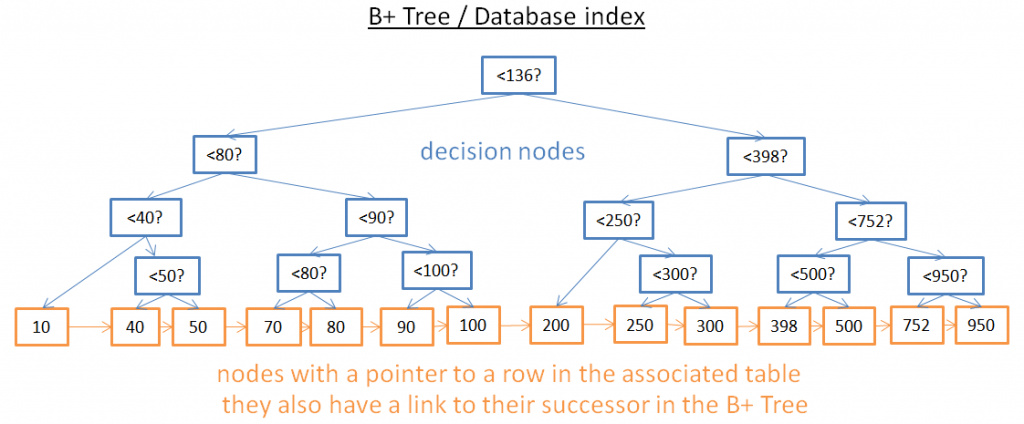
当然会造成节点的数量更多, 但是这个树的深度只是增加了1, 即使是从中搜索某个特定的值, 时间复杂度仍然是O(log2(n))
使用这个树 , 比如要查找[40,100]之间的数据
那么首先找40即可(如果没有40, 就找40之后最接近的一个, 然后沿着叶子节点的链表结构依次向后遍历, 直到遇到一个比100大的数)
数据的增加与删除
解决了数据查询的问题, 但是一定会给数据的增加和删除带来额外的负担, 因为必须要维护B+树的结构, 否则查询的复杂度就会增加, 甚至会失败
也就是说这棵二叉树的子树必须尽可能匀称, 才能保证最佳的查询效率
如果一边偏重, 复杂度就会增加, 甚至极端的情况, 它整体成为了一个链表, 也就是对于每个节点, 它下方的所有节点均在其一棵子树上
那么就会彻底失去意义
B+树本身内置了自我整理和自我平衡的相关算法, 在这里暂且不做详细介绍
插入和删除对B+树的维护都是O(log2(n))的复杂度
所以对于一个表, 不宜创建太多的索引
哈希表
这种数据结构与Java当中的HashMap实现原理基本相同
只不过作为一个对象是在内存当中的
数据库存储和管理数据, 可以将硬盘存储于内存存储相结合
如果有了好的哈希函数(尽最大可能减少哈希冲突), 哈希表查找的时间复杂度是 O(1)
- 一个哈希表可以只装载一半到内存, 剩下的哈希桶可以留在硬盘上
- 如果要使用阵列, 则基于数组的结构需要连续的内存空间 , 如果数据量庞大 , 则很难分配到足够的内存空间
- 使用哈希表可以根据需要选择关键字